UNIVERSIDAD DE  PANAMÁ

FACULTAD DE CIENCIAS NATURALES, EXACTAS Y TECNOLOGÍA 

DEPARTAMENTO DE MATEMÁTICA

PRIMER NIVEL

AÑO 2002

 

 

Nombre ______________________________  Cédula __________________________

 

Lea cuidadosamente cada uno de los enunciados de los problemas. Resuelva de manera completa cada problema en la hoja para cálculos. Escoja la respuesta correcta y señálela en la hoja de respuestas.

 

 

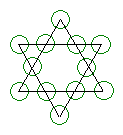
1.                  El número de colores necesarios para colorear los círculos de la figura, de manera tal que dos círculos próximos no tengan el mismo color es:

 

a)  2                 b)  3                 c)  4                 d)  5                 e)  6

 

 

 

 

 

 

 

  

 

 

2.         ¿Cuántas de las siguientes expresiones son ciertas?

         i)        ii)  3% = 0.3    iii)            iv) 

 

a)  cuatro          b)  tres             c)  dos              d)  una              e)  ninguna

 

 

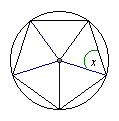
3.         En la figura se muestra un pentágono regular dibujado dentro de un círculo, la medida del ángulo x es: 

 

 a)  54°             b)  60°             c)  70°              d)  72°             e)   75°

 

 

 

 

 

 

 

 

 

 4.      ¿ Cuál de las potencias siguientes tiene mayor valor?

 

a)  2³²               b)  4¹⁵              c)  8¹¹               d) 16⁸               e)  32⁶   

 

                       

5.         La diferencia entre la suma de todos los números pares hasta 2002 y la suma de todos los números impares hasta el 2002 es:

 

a)  0                 b)  1000           c)  1001           d)  2001           e)  2002

 

 

6.         Juan es 8 cm más alto que José. Carlos mide 120 mm menos que Juan.  José mide 12.5 dm. La estatura de Carlos en cm es:

 

a)  145            b)  129            c)  121            d)  113             e)  105

 

7.         Se construyen círculos en el interior de un rectángulo de altura 10 cm, de manera que tocan a la base de éste en un sólo punto. La mayor área posible para uno de estos círculos es:

 

a)    5                              b)    10                            c)  15  

d)  25                              e)  100

 

 

8.                  Cuando un barril está 30% vacío contiene 30 galones más que cuando está  30% lleno. El número de galones que contiene cuando está lleno es:

 

            a)  75               b)  90               c)  100             d)  105             e)  130

 

 

9.         Un bloque en una pirámide de Egipto mide 180 cm de ancho, 504 cm de largo y 396 cm de altura. La medida en cm de la vara de mayor longitud con que un arqueólogo puede medir de manera exacta las dimensiones  del bloque es:

 

a) 12                b)  18               c)  24               d)  36               e)  48

 

 

10.       En la figura se ha sombreado  del cuadrado pequeño y  del cuadrado grande. La razón entre el área sombreada del cuadrado pequeño y el área sombreada del cuadrado grande es:

 

 a)  1/2             b)  4/7              c)  3/4              d)  6/7              e)  7/8

 

 

 

 

 

 

 

 

11.       ¿Cuál de las figuras siguientes tienen mayor perímetro?

 

a)      Un cuadrado de lado 3 cm

b)      Una circunferencia de diámetro 4 cm

c)      Un triángulo rectángulo cuyos catetos miden 3 cm y 4 cm respectivamente

d)      Un rectángulo de área 16 cm²

e)      Un triángulo  equilátero de lado 4½  cm

 

 

12.       ƒABCD es un cuadrado, P y Q son puntos exteriores al cuadrado tales que los triángulos DAPB y DBQC son equiláteros. La medida del ángulo  PQB es:

 

a)  30°              b)  25°             c)  20°              d)  15°             e)  10°

 

 

13.       Un planeta de un sistema solar posee dos satélites naturales, luna A y luna B. Sus movimientos de traslación son tales que la alineación sol-planeta-luna A ocurre cada 18 años, mientras que la alineación sol-planeta-luna B ocurre cada 48 años. Si hoy ocurriera la alineación sol-planeta-luna A-luna B, entonces el fenómeno se repetirá dentro de:

 

a)  144 años    b)  96años        c)  66 años       d)  48 años       e)  18 años

 

 

14.       Un rectángulo con lados de medida entera tienen área 48 cm² y perímetro 28 cm.  La medida en cm de la diagonal del rectángulo es:

 

            a)  6                 b)  8                 c)  10               d)  12               e)  14

 

 

15.              Se tiene una balanza de dos platos y tres discos de 1, 2 y 5 libras respectivamente. ¿Cuántos objetos de diferentes pesos pueden balancearse, utilizando solamente estos discos, si los objetos y los discos se pueden colocar  en cualquiera de los dos platos?

 

 

            a)  6                 b)  7                 c)  8                 d)  10            e)  13